Limes (Mathematik): Unterschied zwischen den Versionen
K (LaTeX-Verhuebschungen; Stil. (Eigentlich hätte ich auch noch gerne \textit{\scriptsize Erdbeer} geschrieben, aber der kennt \scriptsize nicht... wie koennte man das loesen?)) |
K |
||
| Zeile 1: | Zeile 1: | ||
Mit dem '''Limes''', [[deutsch]] auch Grenzwert, haben [[Mathematik]]er sich ein [[Mittel]] geschaffen, um trotz eines Arbeitsaufwands <math>W\to 0</math> ein Ergebnis zu erhalten, dessen Berechnung für den Laien beinahe [[unendlich]] lange dauern würde. Dieses geniale [[Kunst]]werk der Optimierung zeigt unverhofft, wie Mathematiker – oder zumindest einige von ihnen – zu kurzzeitigen großartigen Leistungen fähig sind, wenn es dazu führt, dass sie danach umso mehr dem Müßiggang frönen können. | Mit dem '''Limes''', [[deutsch]] auch Grenzwert, haben [[Mathematik]]er sich ein [[Mittel]] geschaffen, um trotz eines Arbeitsaufwands <math>W\to 0</math> ein Ergebnis zu erhalten, dessen Berechnung für den Laien beinahe [[unendlich]] lange dauern würde. Dieses geniale [[Kunst]]werk der Optimierung zeigt unverhofft, wie Mathematiker – oder zumindest einige von ihnen – zu kurzzeitigen großartigen Leistungen fähig sind, wenn es dazu führt, dass sie danach umso mehr dem Müßiggang frönen können. | ||
| − | + | ==Anwendung== | |
| − | Um nun den Limes als mathematisches Symbol darzustellen, wollen wir einfache und für jeden verständliche [[Beispiel]]e anführen: | + | Um nun den Limes als mathematisches Symbol darzustellen, wollen wir einfache und für jeden verständliche [[Beispiel]]e seiner Anwendung anführen: |
| + | ===Algebraische Verwendung=== | ||
<math>\lim_{8\to9} \sqrt{8} = 3</math> | <math>\lim_{8\to9} \sqrt{8} = 3</math> | ||
| − | Verbal bedeutet dies: Kommt die Acht der Neun immer näher, ja unendlich nahe, so ist [[Wurzel]] aus Acht gleich Drei. | + | Verbal bedeutet dies: Kommt die Acht der Neun immer näher, ja unendlich nahe, so ist [[Wurzel]] aus Acht gleich Drei. |
| − | <math>\lim_{a | + | ===Geometrische Verwendung=== |
| + | <math>\lim_{a^2+b^2\to c^2} \gamma = 90</math> | ||
In Worten: Wenn a<sup>2</sup> + b<sup>2</sup> c<sup>2</sup> beliebig nahe kommen, beträgt der [[Winkel]] Gamma im [[Dreieck]] ABC 90 Grad. Hier sieht man, dass der Limes nicht nur in der Algebra, sondern auch in der Geometrie verwendet wird. Beim obigen Beispiel handelt es sich zum Beispiel um eine leicht veränderte Formulierung des Satzes des [[Pythagoras]]. | In Worten: Wenn a<sup>2</sup> + b<sup>2</sup> c<sup>2</sup> beliebig nahe kommen, beträgt der [[Winkel]] Gamma im [[Dreieck]] ABC 90 Grad. Hier sieht man, dass der Limes nicht nur in der Algebra, sondern auch in der Geometrie verwendet wird. Beim obigen Beispiel handelt es sich zum Beispiel um eine leicht veränderte Formulierung des Satzes des [[Pythagoras]]. | ||
<math>\lim_{a\to b} \ ab = \textit{Quadrat}</math> | <math>\lim_{a\to b} \ ab = \textit{Quadrat}</math> | ||
Hier tritt wieder eine geometrische Verwendung auf, diesmal im Zusammenhang mit dem [[Rechteck]] AB. Wenn die Seite a sich hierbei der Seite b beliebig weit annähert, ist das Rechteck ein [[Quadrat]]. | Hier tritt wieder eine geometrische Verwendung auf, diesmal im Zusammenhang mit dem [[Rechteck]] AB. Wenn die Seite a sich hierbei der Seite b beliebig weit annähert, ist das Rechteck ein [[Quadrat]]. | ||
| + | ===Kulinarische Verwendung=== | ||
<math>\lim_{Erdbeer\to 2\ell} \ </math>[[Bild:Golden Kamel.jpg]] = [[Bild:Kotzing kamel.gif]] | <math>\lim_{Erdbeer\to 2\ell} \ </math>[[Bild:Golden Kamel.jpg]] = [[Bild:Kotzing kamel.gif]] | ||
Heißt: nähert sich der Erdbeer-Limes Konsum der Zwei-Liter-Grenze, so kommt es üblicherweise zum [[Erbrechen]]. | Heißt: nähert sich der Erdbeer-Limes Konsum der Zwei-Liter-Grenze, so kommt es üblicherweise zum [[Erbrechen]]. | ||
| − | + | ===Sonstige=== | |
| − | |||
| − | == | ||
| − | |||
Richtige Anwendung durch ein Kamel: | Richtige Anwendung durch ein Kamel: | ||
| Zeile 21: | Zeile 21: | ||
<math>\lim_{x\to5} \frac{1}{x-5} = </math>[[Bild:rotated5.png]] | <math>\lim_{x\to5} \frac{1}{x-5} = </math>[[Bild:rotated5.png]] | ||
| − | + | {{sa}}[[Limes]], [[Limonade]] | |
| − | + | [[Kategorie: Mathematik]] | |
| − | {{sa}}[[Limes]] | ||
| − | |||
{{hw}} | {{hw}} | ||
| − | |||
| − | |||
Version vom 28. September 2007, 15:50 Uhr
Mit dem Limes, deutsch auch Grenzwert, haben Mathematiker sich ein Mittel geschaffen, um trotz eines Arbeitsaufwands <math>W\to 0</math> ein Ergebnis zu erhalten, dessen Berechnung für den Laien beinahe unendlich lange dauern würde. Dieses geniale Kunstwerk der Optimierung zeigt unverhofft, wie Mathematiker – oder zumindest einige von ihnen – zu kurzzeitigen großartigen Leistungen fähig sind, wenn es dazu führt, dass sie danach umso mehr dem Müßiggang frönen können.
Anwendung
Um nun den Limes als mathematisches Symbol darzustellen, wollen wir einfache und für jeden verständliche Beispiele seiner Anwendung anführen:
Algebraische Verwendung
<math>\lim_{8\to9} \sqrt{8} = 3</math>
Verbal bedeutet dies: Kommt die Acht der Neun immer näher, ja unendlich nahe, so ist Wurzel aus Acht gleich Drei.
Geometrische Verwendung
<math>\lim_{a^2+b^2\to c^2} \gamma = 90</math>
In Worten: Wenn a2 + b2 c2 beliebig nahe kommen, beträgt der Winkel Gamma im Dreieck ABC 90 Grad. Hier sieht man, dass der Limes nicht nur in der Algebra, sondern auch in der Geometrie verwendet wird. Beim obigen Beispiel handelt es sich zum Beispiel um eine leicht veränderte Formulierung des Satzes des Pythagoras.
<math>\lim_{a\to b} \ ab = \textit{Quadrat}</math>
Hier tritt wieder eine geometrische Verwendung auf, diesmal im Zusammenhang mit dem Rechteck AB. Wenn die Seite a sich hierbei der Seite b beliebig weit annähert, ist das Rechteck ein Quadrat.
Kulinarische Verwendung
<math>\lim_{Erdbeer\to 2\ell} \ </math> =
= 
Heißt: nähert sich der Erdbeer-Limes Konsum der Zwei-Liter-Grenze, so kommt es üblicherweise zum Erbrechen.
Sonstige
Richtige Anwendung durch ein Kamel:
<math>\lim_{x\to8} \frac{1}{x-8} = \infty</math>
Fehlinterpretation eines Dromedars:
<math>\lim_{x\to5} \frac{1}{x-5} = </math>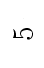
![]() Siehe auch: Limes, Limonade
Vorlage:Hw
Siehe auch: Limes, Limonade
Vorlage:Hw