Primzahl: Unterschied zwischen den Versionen
(so jetzt aber *koppschüttel*) |
WiMu (Diskussion | Beiträge) K |
||
| (17 dazwischenliegende Versionen von 15 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | ''Primzahlen'' sind die ersten [[Zahl]]en, die es gab. Die allererste Zahl war die [[2]]. Die 1 wurde erst | + | ''Primzahlen'' sind die ersten [[Zahl]]en, die es gab. Die allererste Zahl war die [[2]]. Die 1 wurde erst viel später entdeckt (siehe weiter unten), wer bräuchte sie auch, wenn man noch nicht weiterzählen kann. Nach der zwei wurde von [[Indien|indischen]] Kamelen die drei entdeckt, die erste große Erungenschaft der [[Mathematik]]. Damit waren alle Kamele fürs erste zufrieden, denn damit konnte man sowohl die Anzahl der Höcker eines Kamels zählen und zugleich der Behauptung widersprechen, dass Kamele nicht bis 3 zählen könnten. |
| − | Irgendwann machten sich dann die [[Mathematiker]] über die Zahlen her und fragten sich, was passiert, wenn man alle bekannten Zahlen addiert und entdeckten so die 5. Danach versuchten sie das gleiche nochmal, entdeckten dabei aber nicht die 10, sondern weil sie vegessen haben die drei hinzuzuzählen die 7. Als sie merkten, | + | Irgendwann machten sich dann die [[Mathematiker]] über die Zahlen her und fragten sich, was passiert, wenn man alle bekannten Zahlen addiert und entdeckten so die 5. Danach versuchten sie das gleiche [[Dejawüste|nochmal]], entdeckten dabei aber nicht die 10, sondern weil sie vegessen haben die drei hinzuzuzählen die 7. Als sie merkten, dass sie die 3 vergessen hatten, zählten zwei Mathematiker gleichzeitig die 3 dazu und entdeckten so die 13. Es dauerte danach nicht lange, bis eine äußerst einfache Rekursionsformel für Zahlen entdeckt wurde, die sofort die nächsten Zahlen lieferte: 17, 19, 23, 29,... |
| − | Ein besondere Rolle nimmt die Primzahl '''11''' ein, da sie außerdem noch eine absolut trinkfeste [[Schnapszahl]] ist. Die einzige Primzahl ihrer Art (wenn man mal von 1111111111111111111, 11111111111111111111111 und einigen unanständig großen Zahlen absieht) [[#(0)|(0)]]. Kamele die zu oft einer '''11''' begegnen können leicht sozial abrutschen und zum [[Nieselpriem|Nieselprim]] mutieren. Und da Mathematiker nicht trinken oder wenn sie trinken nicht denken, konnte die 11 erst relativ spät entdeckt werden. | + | Ein besondere Rolle nimmt die Primzahl '''11''' ein, da sie außerdem noch eine absolut trinkfeste [[Schnapszahl]] ist. Die einzige Primzahl ihrer Art (wenn man mal von 1111111111111111111, 11111111111111111111111 und einigen unanständig großen Zahlen absieht) [[#(0)|(0)]]. Kamele, die zu oft einer '''11''' begegnen, können leicht [[Sozia|sozial]] abrutschen und zum [[Nieselpriem|Nieselprim]] mutieren. Und da Mathematiker nicht trinken oder wenn sie trinken nicht denken, konnte die 11 erst relativ spät entdeckt werden. |
Die '''11''' im Pascalschen Dreieck:<br>[[Bild:B-1hochN-1.png]] --> für 10 = B; 11 = B + 1 --> [[Bild:11-hoch-N-1.png]]<br> | Die '''11''' im Pascalschen Dreieck:<br>[[Bild:B-1hochN-1.png]] --> für 10 = B; 11 = B + 1 --> [[Bild:11-hoch-N-1.png]]<br> | ||
Vernüpfung der i Elemente der n-ten Zeile im Pascalschen Dreieck unter Verwendung eines Zahlenssystems mit der Basis B. Darstellung unter Verwendung der Ziffern 0, 1, ... (B-1).<br> | Vernüpfung der i Elemente der n-ten Zeile im Pascalschen Dreieck unter Verwendung eines Zahlenssystems mit der Basis B. Darstellung unter Verwendung der Ziffern 0, 1, ... (B-1).<br> | ||
| Zeile 18: | Zeile 18: | ||
8 1 11 33 55 55 33 11 1 25352411= '''11^7''' 823543 = 7^7 Pa amel | 8 1 11 33 55 55 33 11 1 25352411= '''11^7''' 823543 = 7^7 Pa amel | ||
{| | {| | ||
| − | | [[Bild:Öhm.png | + | | [[Bild:Öhm.png|left]] |
| − | | Es treiben sich, gut getarnt, zumeist extraterestrische '''11'''en herum, die ganz und gar nicht primzahlig sind! Neben: 11<sub>binär</sub> = 3<sub>dezimal</sub> = Prim; 11<sub>heximal</sub> = 7<sub>dezimal</sub> = Prim und 11<sub>hexadezimal</sub> = 17<sub>dezimal</sub> = Prim; gibt es auch sogenannte "falsche Elfer" wie: 11<sub>oktal</sub> = 9<sub>dezimal</sub> = 3*3 ! und 11<sub>13</sub> = 14<sub>dezimal</sub> = 2*7 !, Don't Panic! [[#(1)|(1)]]. | + | | Es treiben sich, gut getarnt, zumeist extraterestrische '''11'''en herum, die ganz und gar nicht primzahlig sind! Neben: 11<sub>binär</sub> = 3<sub>dezimal</sub> = Prim; 11<sub>heximal</sub> = 7<sub>dezimal</sub> = Prim und 11<sub>hexadezimal</sub> = 17<sub>dezimal</sub> = Prim; gibt es auch sogenannte "falsche Elfer" wie: 11<sub>oktal</sub> = 9<sub>dezimal</sub> = 3*3 ! und 11<sub>13</sub> = 14<sub>dezimal</sub> = 2*7 !,11<sub>rektal</sub>= 10<sub>dezimal</sub> Don't Panic! [[#(1)|(1)]]. |
|} | |} | ||
| − | So hatten die Mathematiker zwar [[unendlich]] viele Zahlen entdeckt, waren aber der Meinung, | + | So hatten die Mathematiker zwar [[unendlich]] viele Zahlen entdeckt, waren aber der Meinung, dass da noch welche fehlten. Das dadurch berühmt gewordene Kamel [[Fermat]] entdeckte etwa 500 Jahre nach der Rekursionsformel für Zahlen eine weitere Zahl: Die [[1]]. Um sie von den älteren Zahlen zu unterscheiden, nannte er die älteren Zahlen als die ersten Zahlen, also Primzahlen und schrieb dann den als Fermats letzter Satz berühmtgewordenen Satz auf den Rand des Krimis, den er gerade las "1 ist keine Primzahl". |
Allerdings blieb es noch lange danach unklar, ob es noch weitere Nichtprimzahlen gab. Erst 1997 konnte ein ergänzender Beweis zu Fermats letzten Satz vorgelegt werden, der noch 419 weitere Nichtprimzahlen aufzeigte. Seitdem kann man ohne auf Zahllücken zu stoßen bis 517 zählen. | Allerdings blieb es noch lange danach unklar, ob es noch weitere Nichtprimzahlen gab. Erst 1997 konnte ein ergänzender Beweis zu Fermats letzten Satz vorgelegt werden, der noch 419 weitere Nichtprimzahlen aufzeigte. Seitdem kann man ohne auf Zahllücken zu stoßen bis 517 zählen. | ||
Größere Nichtprimzahlen konnten noch nicht gefunden werden, da diese Zahlen über[[abzählbar]] endlich werden. Im Rahmen des GIMPS-Projektes werden solche Nichtprimzahlen gesucht. Auf die erste Nichtprimzahl mit mehr als 3 Stellen ist eine Belohnung von 1000003 [[Teuro]] ausgesetzt. | Größere Nichtprimzahlen konnten noch nicht gefunden werden, da diese Zahlen über[[abzählbar]] endlich werden. Im Rahmen des GIMPS-Projektes werden solche Nichtprimzahlen gesucht. Auf die erste Nichtprimzahl mit mehr als 3 Stellen ist eine Belohnung von 1000003 [[Teuro]] ausgesetzt. | ||
| + | |||
| + | {{nv}} [[Primelzahl]] | ||
---- | ---- | ||
| Zeile 34: | Zeile 36: | ||
Selbstverständlich leugnet auch Douglas Adams, der Schreiber des Romans "[[Per Anhalter durch Ägypten|Per Anhalter durch die Galaxis]]" jeglichen Bezug der Zahl 42 zur Zahlenbasis 13, aber das ist nur ein Trick der Außerirdischen, um die Kamele zu verwirren. | Selbstverständlich leugnet auch Douglas Adams, der Schreiber des Romans "[[Per Anhalter durch Ägypten|Per Anhalter durch die Galaxis]]" jeglichen Bezug der Zahl 42 zur Zahlenbasis 13, aber das ist nur ein Trick der Außerirdischen, um die Kamele zu verwirren. | ||
| − | {{sa}} [[54]], [[42]], [[Frage]] und [[Per Anhalter durch Ägypten]] | + | {{sa}} [[54]], [[42]], [[Frage]] und [[Per Anhalter durch Ägypten]], [[Primzahlenraupe]] |
| + | |||
| + | ===(2)=== | ||
| + | Ich vermute, dass es ein Konstruktionsprinzip für Nichtprimzahlen gibt. Mein erster Versuch hierfür war: Für alle Primzahlen p gibt es ein n = p + 1, so dass n eine Nichtprimzahl ist. Leider bin ich nicht bewandert genug, um dies zu beweisen, aber vielleicht gelingt das ja jemand anderem. Denn fast jede Primzahl ungerade, wenn man nun 1 hinzuzählt, wird die Zahl gerade, so dass sie durch 2 teilbar ist. Allerdings gibt es hier ein Gegenbeispiel, nämlich ist die 2 bereits gerade, so dass beim Hinzuzählen von 1 erneut eine Primzahl herauskommt. Das beweist einmal mehr die Wichtigkeit der Entdeckung der 2 und der 3. | ||
| + | Oder so. | ||
| + | |||
| + | |||
| + | {{zahlen}} | ||
| + | |||
| + | [[stupi:Primzahl]] | ||
| + | [[uncy:Primzahl]] | ||
| + | [[uncy-en:Prime number]] | ||
| + | [[wiki:Primzahl]] | ||
| + | [[wiki-en:Prime number]] | ||
[[Kategorie:Zahl]] | [[Kategorie:Zahl]] | ||
[[Kategorie:Mathematik]] | [[Kategorie:Mathematik]] | ||
Aktuelle Version vom 13. Mai 2011, 22:00 Uhr
Primzahlen sind die ersten Zahlen, die es gab. Die allererste Zahl war die 2. Die 1 wurde erst viel später entdeckt (siehe weiter unten), wer bräuchte sie auch, wenn man noch nicht weiterzählen kann. Nach der zwei wurde von indischen Kamelen die drei entdeckt, die erste große Erungenschaft der Mathematik. Damit waren alle Kamele fürs erste zufrieden, denn damit konnte man sowohl die Anzahl der Höcker eines Kamels zählen und zugleich der Behauptung widersprechen, dass Kamele nicht bis 3 zählen könnten.
Irgendwann machten sich dann die Mathematiker über die Zahlen her und fragten sich, was passiert, wenn man alle bekannten Zahlen addiert und entdeckten so die 5. Danach versuchten sie das gleiche nochmal, entdeckten dabei aber nicht die 10, sondern weil sie vegessen haben die drei hinzuzuzählen die 7. Als sie merkten, dass sie die 3 vergessen hatten, zählten zwei Mathematiker gleichzeitig die 3 dazu und entdeckten so die 13. Es dauerte danach nicht lange, bis eine äußerst einfache Rekursionsformel für Zahlen entdeckt wurde, die sofort die nächsten Zahlen lieferte: 17, 19, 23, 29,...
Ein besondere Rolle nimmt die Primzahl 11 ein, da sie außerdem noch eine absolut trinkfeste Schnapszahl ist. Die einzige Primzahl ihrer Art (wenn man mal von 1111111111111111111, 11111111111111111111111 und einigen unanständig großen Zahlen absieht) (0). Kamele, die zu oft einer 11 begegnen, können leicht sozial abrutschen und zum Nieselprim mutieren. Und da Mathematiker nicht trinken oder wenn sie trinken nicht denken, konnte die 11 erst relativ spät entdeckt werden.
Die 11 im Pascalschen Dreieck: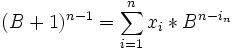 --> für 10 = B; 11 = B + 1 -->
--> für 10 = B; 11 = B + 1 --> 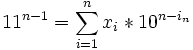
Vernüpfung der i Elemente der n-ten Zeile im Pascalschen Dreieck unter Verwendung eines Zahlenssystems mit der Basis B. Darstellung unter Verwendung der Ziffern 0, 1, ... (B-1).
Beispiel mit Heximaler Basis B (0,1,2,3,4,5):
Heximal Dezimal n=1 1 1= 11^0 1 = 7^0 2 1 1 11= 11^1 7 = 7^1 3 1 2 1 121= 11^2 49 = 7^2 4 1 3 3 1 1331= 11^3 343 = 7^3 5 1 4 10 4 1 15041= 11^4 2401 = 7^4 6 1 5 14 14 5 1 205451= 11^5 16807 = 7^5 lshe 7 1 10 23 32 23 10 1 2304401= 11^6 117649 = 7^6 sca es K 8 1 11 33 55 55 33 11 1 25352411= 11^7 823543 = 7^7 Pa amel
| Es treiben sich, gut getarnt, zumeist extraterestrische 11en herum, die ganz und gar nicht primzahlig sind! Neben: 11binär = 3dezimal = Prim; 11heximal = 7dezimal = Prim und 11hexadezimal = 17dezimal = Prim; gibt es auch sogenannte "falsche Elfer" wie: 11oktal = 9dezimal = 3*3 ! und 1113 = 14dezimal = 2*7 !,11rektal= 10dezimal Don't Panic! (1). |
So hatten die Mathematiker zwar unendlich viele Zahlen entdeckt, waren aber der Meinung, dass da noch welche fehlten. Das dadurch berühmt gewordene Kamel Fermat entdeckte etwa 500 Jahre nach der Rekursionsformel für Zahlen eine weitere Zahl: Die 1. Um sie von den älteren Zahlen zu unterscheiden, nannte er die älteren Zahlen als die ersten Zahlen, also Primzahlen und schrieb dann den als Fermats letzter Satz berühmtgewordenen Satz auf den Rand des Krimis, den er gerade las "1 ist keine Primzahl".
Allerdings blieb es noch lange danach unklar, ob es noch weitere Nichtprimzahlen gab. Erst 1997 konnte ein ergänzender Beweis zu Fermats letzten Satz vorgelegt werden, der noch 419 weitere Nichtprimzahlen aufzeigte. Seitdem kann man ohne auf Zahllücken zu stoßen bis 517 zählen.
Größere Nichtprimzahlen konnten noch nicht gefunden werden, da diese Zahlen überabzählbar endlich werden. Im Rahmen des GIMPS-Projektes werden solche Nichtprimzahlen gesucht. Auf die erste Nichtprimzahl mit mehr als 3 Stellen ist eine Belohnung von 1000003 Teuro ausgesetzt.
![]() Nicht zu verwechseln mit: Primelzahl
Nicht zu verwechseln mit: Primelzahl
(0)[<small>bearbeiten</small>]
Echte Schnapszahlen sind natürlich zweistellig bzw. dreistellig. Bei 1111...en etc. handelt es sich genau genommen um Bierzahlen. Das wird aber oft in der Trinkerpraxis nicht so genau genommen.
(1)[<small>bearbeiten</small>]
Selbstverständlich leugnet auch Douglas Adams, der Schreiber des Romans "Per Anhalter durch die Galaxis" jeglichen Bezug der Zahl 42 zur Zahlenbasis 13, aber das ist nur ein Trick der Außerirdischen, um die Kamele zu verwirren.
![]() Siehe auch: 54, 42, Frage und Per Anhalter durch Ägypten, Primzahlenraupe
Siehe auch: 54, 42, Frage und Per Anhalter durch Ägypten, Primzahlenraupe
(2)[<small>bearbeiten</small>]
Ich vermute, dass es ein Konstruktionsprinzip für Nichtprimzahlen gibt. Mein erster Versuch hierfür war: Für alle Primzahlen p gibt es ein n = p + 1, so dass n eine Nichtprimzahl ist. Leider bin ich nicht bewandert genug, um dies zu beweisen, aber vielleicht gelingt das ja jemand anderem. Denn fast jede Primzahl ungerade, wenn man nun 1 hinzuzählt, wird die Zahl gerade, so dass sie durch 2 teilbar ist. Allerdings gibt es hier ein Gegenbeispiel, nämlich ist die 2 bereits gerade, so dass beim Hinzuzählen von 1 erneut eine Primzahl herauskommt. Das beweist einmal mehr die Wichtigkeit der Entdeckung der 2 und der 3. Oder so.
[]
stupi:Primzahl uncy:Primzahl uncy-en:Prime number wiki:Primzahl wiki-en:Prime number
