Eineck: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
K (Ah, Kotz-Bindestrichminus... Taste abhacken!!!) |
K |
||
| (12 dazwischenliegende Versionen von 9 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Ein '''Eineck''' ist ein Polygon (n-Eck) mit genau einem Eckpunkt. | + | Ein '''Eineck''' ist ein Polygon (n-Eck) mit genau einem Eckpunkt, also ein Monogon. Aussehen: '''.''' |
| − | |||
| − | Aussehen: | ||
| − | == Besonderheiten == | + | ==Besonderheiten== |
| + | *Jedes Eineck ist konkav, d.h. die Punkte der Verbindungsstrecke zweier beliebiger [[Punkt]]e der Figur liegen '''in''' der [[Figur]]. | ||
| + | *Es gibt keine überschlagenen Einecke. | ||
| + | *Das Eineck besitzt nur eine einzige Kante mit der Bezeichnung a, nämlich die für [[Polygon]]e obligatorische Verbindung zwischen dem letzten Punkt (P<sub>n</sub>) und dem ersten Punkt (P<sub>1</sub>). | ||
| + | *Da n, die Anzahl der Punkte, 1 ist, fallen Anfangs- und Endpunkt der [[Kante]] a zusammen, woraus sich für a die Länge 0 ergibt. | ||
| + | *Der Umfang beträgt daher U=a=0. | ||
| + | *Die Fläche beträgt 0 und ergibt sich bei der Triangulation in −1 gleichseitige Dreiecke mit der Kantenlänge 0 und somit auch der Fläche 0. | ||
| + | *Das Volumen beträgt ebenfalls 0. | ||
| + | *Die Innenwinkelsumme eines Einecks beträgt −180° und entzieht sich jeder Anschauung. | ||
| − | + | ==Sonderformen== | |
| − | * | + | [[Datei:Konvexes Eineck.svg|ungerahmt|rechts|Konvexes Eineck]] |
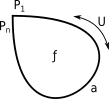
| − | + | Eine Sonderform des Einecks ist das konvexe Eineck. Es erfüllt nahezu alle Kriterien eines Einecks. Jedoch erfährt die Verbindungsstrecke a eine zweidimensionale Auslenkung U entlang der negativen X- und Y-Achsen. | |
| − | * | + | *Die Punkte der Verbindungsstrecke zweier beliebiger [[Punkt]]e der Figur liegen '''außerhalb''' der [[Figur]]. |
| − | * | + | *Konvexe Einecke können sich ausschließlich entlang der '''negativen''' X- und Y-Achsen ausdehnen. |
| − | * | + | *Dehnt sich ein konvexes Eineck entlang der '''positiven''' X- und Y-Achsen aus, handelt es sich um eine [[Explosion]]; die Darstellung desselben folglich um eine Explosionszeichnung. |
| − | + | *Enthält ƒ einen [[Druck|Überdruck]], beschreibt das konvexe Eineck eine [[Kaugummi|Kaugummiblase]]. | |
| − | + | *Das konvexe Eineck ist ein [[Zustand|Zwischenstadium]] der [[Quadratur des Kreises]]. | |
| − | {{sa}} [[Zweieck]] | + | ==Geschichte== |
| + | Das Eineck war schon den alten [[Ägypten]] bekannt. Pharao Osmosis rammte eineckige Pfeiler in den [[Sand]], um daran große [[Pyramide]]n anzuständern. Die Ägypter vervollkommneten die Technik des Ein[[rad]]fahrens später durch Verdrahtung ägyptischer Leuchtpysen. | ||
| + | |||
| + | |||
| + | {{sa}} [[Zweieck]]<br> | ||
| + | {{sv}} [[Dreieck]], [[Viereck]], [[dreieckig]] | ||
| + | |||
| + | [[wiki:Eineck]] | ||
| + | |||
| + | [[Kategorie:Mathematik]] | ||
Aktuelle Version vom 16. August 2020, 09:17 Uhr
Ein Eineck ist ein Polygon (n-Eck) mit genau einem Eckpunkt, also ein Monogon. Aussehen: .
Besonderheiten[<small>bearbeiten</small>]
- Jedes Eineck ist konkav, d.h. die Punkte der Verbindungsstrecke zweier beliebiger Punkte der Figur liegen in der Figur.
- Es gibt keine überschlagenen Einecke.
- Das Eineck besitzt nur eine einzige Kante mit der Bezeichnung a, nämlich die für Polygone obligatorische Verbindung zwischen dem letzten Punkt (Pn) und dem ersten Punkt (P1).
- Da n, die Anzahl der Punkte, 1 ist, fallen Anfangs- und Endpunkt der Kante a zusammen, woraus sich für a die Länge 0 ergibt.
- Der Umfang beträgt daher U=a=0.
- Die Fläche beträgt 0 und ergibt sich bei der Triangulation in −1 gleichseitige Dreiecke mit der Kantenlänge 0 und somit auch der Fläche 0.
- Das Volumen beträgt ebenfalls 0.
- Die Innenwinkelsumme eines Einecks beträgt −180° und entzieht sich jeder Anschauung.
Sonderformen[<small>bearbeiten</small>]
Eine Sonderform des Einecks ist das konvexe Eineck. Es erfüllt nahezu alle Kriterien eines Einecks. Jedoch erfährt die Verbindungsstrecke a eine zweidimensionale Auslenkung U entlang der negativen X- und Y-Achsen.
- Die Punkte der Verbindungsstrecke zweier beliebiger Punkte der Figur liegen außerhalb der Figur.
- Konvexe Einecke können sich ausschließlich entlang der negativen X- und Y-Achsen ausdehnen.
- Dehnt sich ein konvexes Eineck entlang der positiven X- und Y-Achsen aus, handelt es sich um eine Explosion; die Darstellung desselben folglich um eine Explosionszeichnung.
- Enthält ƒ einen Überdruck, beschreibt das konvexe Eineck eine Kaugummiblase.
- Das konvexe Eineck ist ein Zwischenstadium der Quadratur des Kreises.
Geschichte[<small>bearbeiten</small>]
Das Eineck war schon den alten Ägypten bekannt. Pharao Osmosis rammte eineckige Pfeiler in den Sand, um daran große Pyramiden anzuständern. Die Ägypter vervollkommneten die Technik des Einradfahrens später durch Verdrahtung ägyptischer Leuchtpysen.
![]() Siehe auch: Zweieck
Siehe auch: Zweieck
![]() Siehe vielleicht: Dreieck, Viereck, dreieckig
Siehe vielleicht: Dreieck, Viereck, dreieckig